
Lineáris regresszió elemzésének lépései

Mi a lineáris regresszió?
A lineáris regresszió kapcsolatot néz két dolog között.
Mi a különbség a lineáris regresszió és a korreláció között?
A korreláció megmutatja, hogy két dolog összefügg-e, de nem tár fel ok-okozati kapcsolatot. Tehát ha én a Hell Energy marketingese vagyok, és kiderül, hogy aki Candy Crush-ozik, az nagyobb eséllyel vásárol Hell energiaitalt, akkor nyilván reklámozni fogok a Candy Crush játékban. Ettől még nem értem meg, hogy MIÉRT van ez így, tehát nem biztos, hogy a Candy Crush játék szeretete okozza azt, hogy valaki szereti a Hell energiaitalt, és fordítva; a Hell Energy szeretete nem OKOZZA a Candy Crush szeretetét, egyszerűen valamiért van összefüggés, ez nekem hasznos információ, de NEM ok-okozati összefüggés!!!
Ellenben a lineáris regresszió már ok-okozati összefüggés. Tehát X dolog MEGMAGYARÁZ Y dolgot. Tehát ebben az esetben ha a Hell Energy-s példát vesszük, és a lineáris regresszió összefüggést tár fel, az azt jelenti nekünk, hogy a Hell Energy energiaital kedvelése okozza (egy bizonyos mértékben) a Candy Crush játék szeretését is. Ezt az "egy bizonyos mértéket", tehát azt, hogy X dolog milyen mértékben befolyásol Y dolgot, szintén megmutatja a lineáris regresszió. Tehát nem csak azt tudjuk meg, hogy valami hatással van valamire, hanem azt is, hogy mekkora hatással.
Hogyan csinálok lineáris regressziót?
Kijelölök egy úgynevezett függő változót, és egy független, vagy más néven prediktor (predict, mint angolul "megjósolni", "előrejelezni") változót. A függő változó az a valami ami FÜGG a prediktor változótól.
Például azt mondom, hogy kíváncsi vagyok, hogy az, hogy a kiskutyák szeretik-e a gazdájukat, összefügg-e azzal, hogy mennyi jutalomfalatot kapnak.
EZ EGY TELJESEN A VALÓSÁGTÓL ELRUGASZKODOTT PÉLDA, ENNEK MEGFELELŐEN IS KEZELJÉTEK A BEMUTATÁST, KEDVES OLVASÓK, DE A MEGÉRTÉST JELENTŐSEN MEGKÖNNYÍTI.
Ha úgy gondolom, hogy a jutifalik száma hatással van a gazdi kedvelésének mértéke, akkor az lesz prediktor változóm, hogy mennyi jutifalit kapnak (hiszen ez JÓSOLJA meg nekünk, hogy mennyire szeretik a gazdit)
és a gazdi szeretetének mértéke pedig a függő változóm, hiszen az FÜGG az a jutifalik számától. Nem fordítva, tehát az, hogy a kutyák mennyire szeretik a gazdit, nem lehet prediktora a jutifalik számának, mert hát nem a kutya határozza meg, mennyi jutifalit kap ő maga.
Tehát ennyi a lényeg, két dolog kell hozzá, egy prediktor és egy függő változó. Mindkettő egy szám adat, nominális (azaz szöveges) adatokat nem tud kezelni a lineáris regresszió (van olyan módszer, ami tud szöveges adatot kezelni, de nem ez releváns jelenleg a számunkra).
Vegyük a példánkat.
H1: Minél több jutifalit ad egy gazdi a kutyusának, a kutyus annál jobban szereti őt.
Azt, hogy ezt a hipotézist hogyan is találhatjuk ki, itt írtam le.
Mint mondtuk, két változó kell: függő, és független. A függő változónk ez esetben az, hogy a kutyus mennyire szereti a gazdit. A független, azaz prediktor változó, ami megjósolja az érzelmi elkötelezettséget, az pedig a kapott jutifalatok száma.
Honnan vettük a függő és a független változóinkat? Független: megkérdeztük a gazdikat, mennyi jutifalit adnak a kutyusuknak. Függő: hányszor csóválja a kiskutya a farkát, amikor meglátja a gazdit. Fogunk X darab (mondjuk 100) kutyagazdit, és megkérdezzük:
1) Ön hányszor ad egy héten jutalomfalatot kiskutyájának?
2) Az Ön kiskutyája hányszor csóválja a farkát egy héten? (Azt, hogy mégis mi alapján találtuk ki ezt a kérdést, és miért nem mást kérdeztünk, itt írtam le).
Nos, ez után Így néznek ki a kapott adatok.
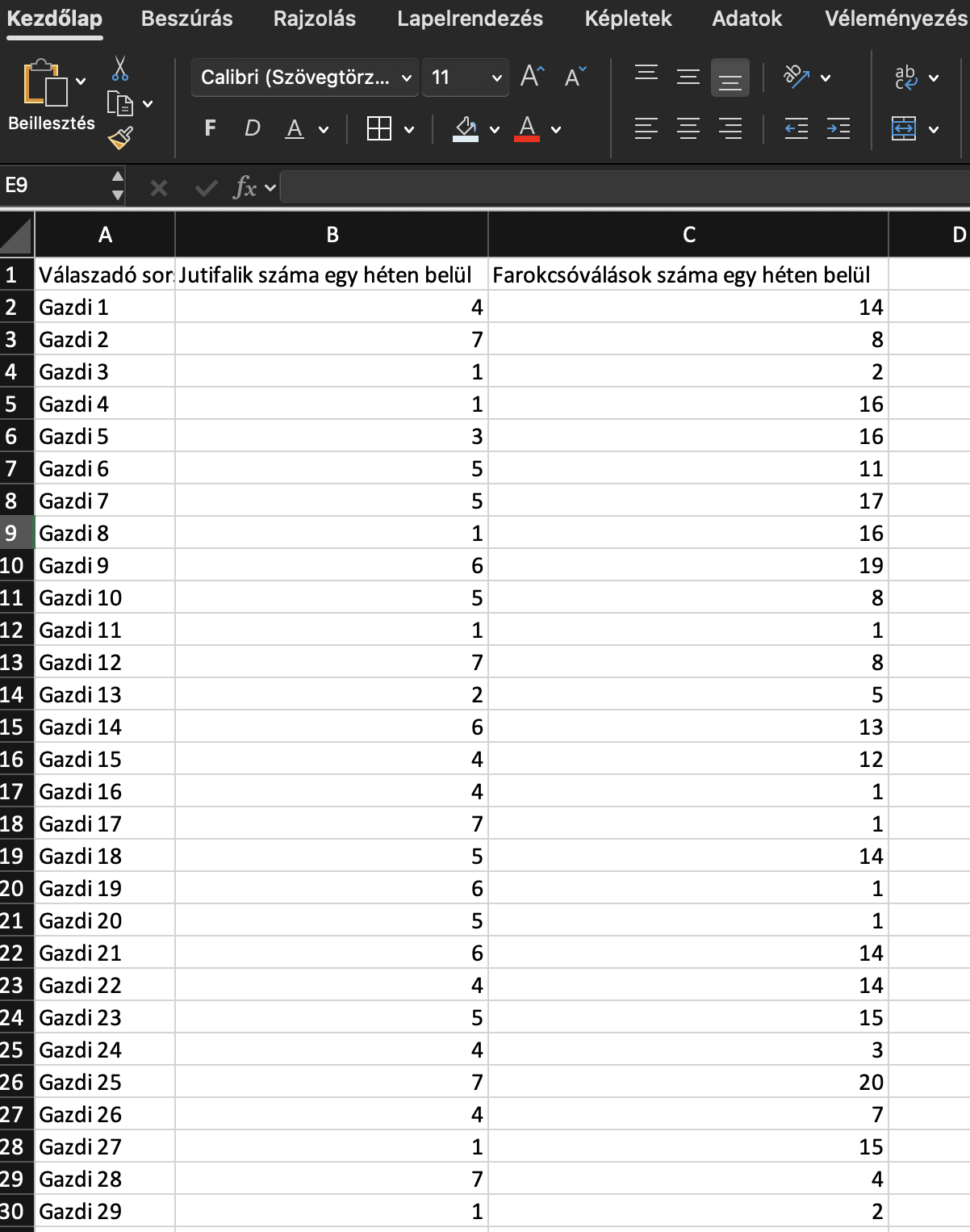
Tehát megnézzük, hogy konzekvensen ugyanúgy alakulnak-e az adatok a gazdiknál. Ha minél több gazdinál előfordul, hogy minél több jutifalit ad, annál több a farokcsóválások száma, annál erősebb a kapcsolat. Tehát megnézzük, mennyire mozognak egy irányba az adatok.
fogtuk az összes válaszadónak a két átlag pontszámát, és így rendeztük. (Ez egy példa.)
Értelemszerűen a táblázat sokkal több sorból áll, hiszen több válaszadónk van. E között a két "oszlop" (hivatalos megnevezéssel változó) között számolunk összefüggést.
A lineáris regresszió output-ja valahogy így néz ki, lásd a következő képen (ez programtól függően egy kicsit eltérhet, pl. más háttérszín, vagy betűtípus, de összességében ezeket a táblázatokat fogja tartalmazni). Az "output" a statisztikai programokban az eredmények ablaka/fájlja – minden, amit a futtatott elemzés "kiad": táblák, ábrák, számok, figyelmeztetések. Olyan, mint egy jegyzőkönyv arról, mit kértél a programtól és mit számolt ki. Nem a nyers adatok, hanem az eredmények összefoglalója.
A lineáris regresszió output-ja
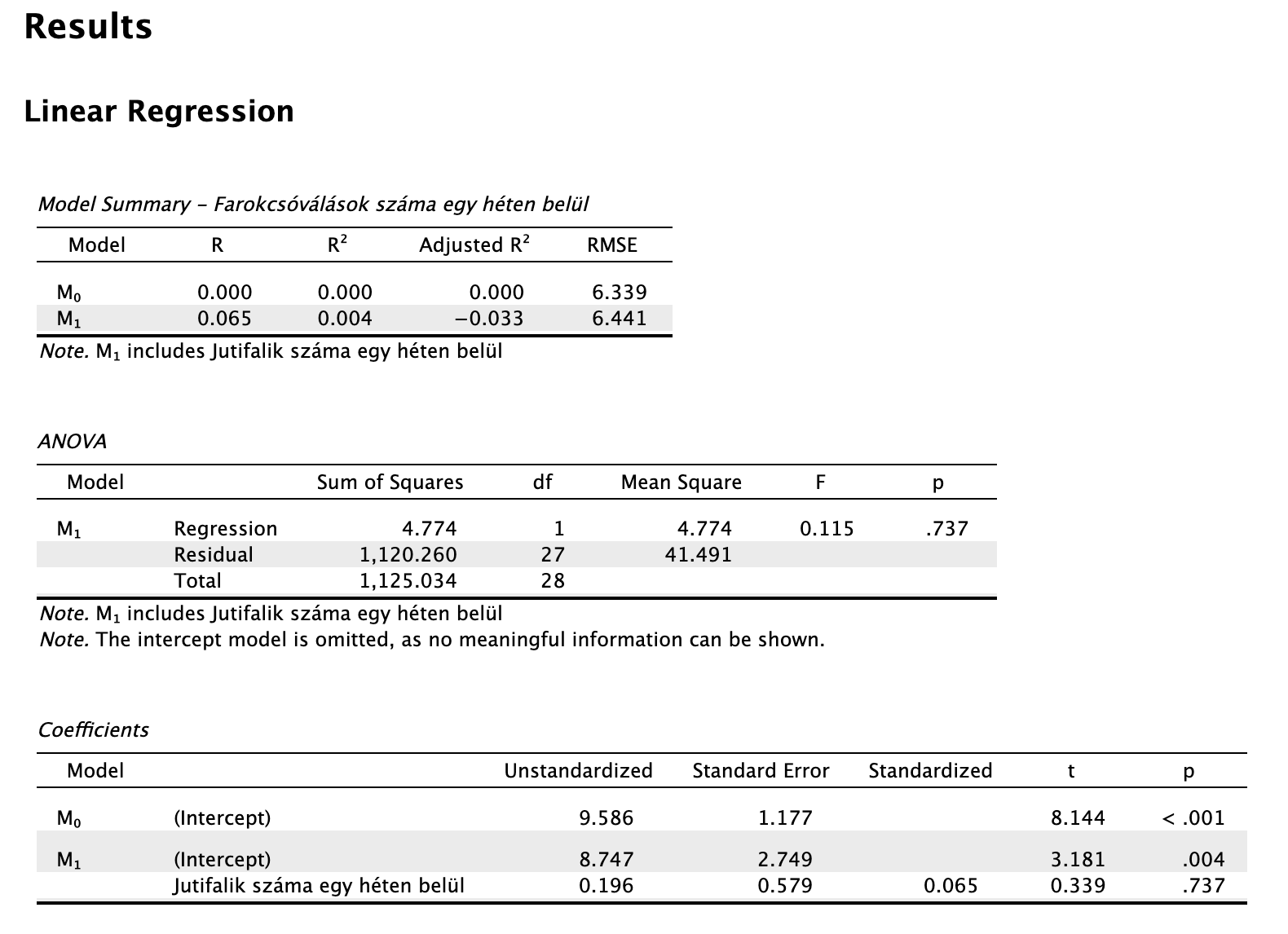
A lineáris regresszió eredmények értelmezésének menete
Ennek a két oszlopnak az összefüggéseinek a vizsgálata 3 táblázatot fog eredményezni. A lineáris regresszió output-ja 3 táblázatból áll: egy ANOVA táblázatból, egy Modell summary, és egy coefficiens táblázatból.
ANOVA táblázat
1) Az első lépés mindig az ANOVA F-tesztjének p-értéke (a táblázat legutolsó oszlopa mindig, az oszlop címe "p")
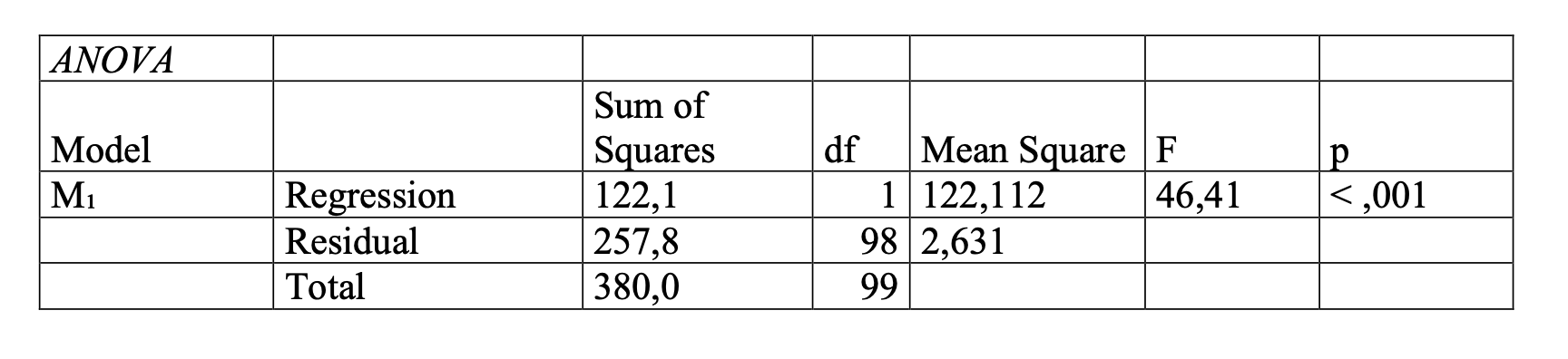
A p-érték mutatja a szignfikanciaszintet. Arról, hogy mi a szignifikanciaszint, itt írtunk.
Ha a p-érték 0,05 (azaz 5 százalék) alatt van, az azt jelenti, hogy az eredmény szignifikáns, ergó a lineáris regressziós modell eredményei általánosíthatók a populációra, és érdemes a lineáris regressziós modellel dolgozni. Ha nem szignifkáns, azaz nagyobb, mint 0,05; akkor kész, vége is van az elemzésnek, a másik két táblázatra rá se nézünk, csókolom. Hiszen nem szignfikáns, mit csináljunk vele? semmit. Leírjuk, hogy nincs összefüggés, a hipotézist nem sikerült igazolni, és annyi. DE! ha szignifikáns, folytatjuk az eredmények elemzését. Ha szignifikáns, akkor nézzük a következő két táblázatot, a "model summary", azaz a modell összefoglaló táblázatot.
Miért hívjuk modellnek? A lineáris regresszió kvázi modellezni próbál: azt feltételezzük, hogy két darab adat (pl. a nagymamák életkora és a sütemény sütési kedv) együtt mozognak. Természetesen ilyen tökéletes együttmozgás a valóságban nincs. Mi adunk neki adatokat, amelyek szintén adnak egy modellt – tehát két adatot, amely valamilyen mértékben együtt mozog vagy éppen nem mozog együtt. Ha ez az együttmozgás láthatóan mintázatot követ, működik, akkor érdemes vele dolgozni, mert nem véletlenszerűen alakultak úgy az adatok, hanem abszolút racionális feltételezés, hogy ezek együtt mozognak.
Modell summary (modell összefoglaló táblázat) a lineáris regresszióban
2) Tehát ez után a "modell summary" táblázat következik.
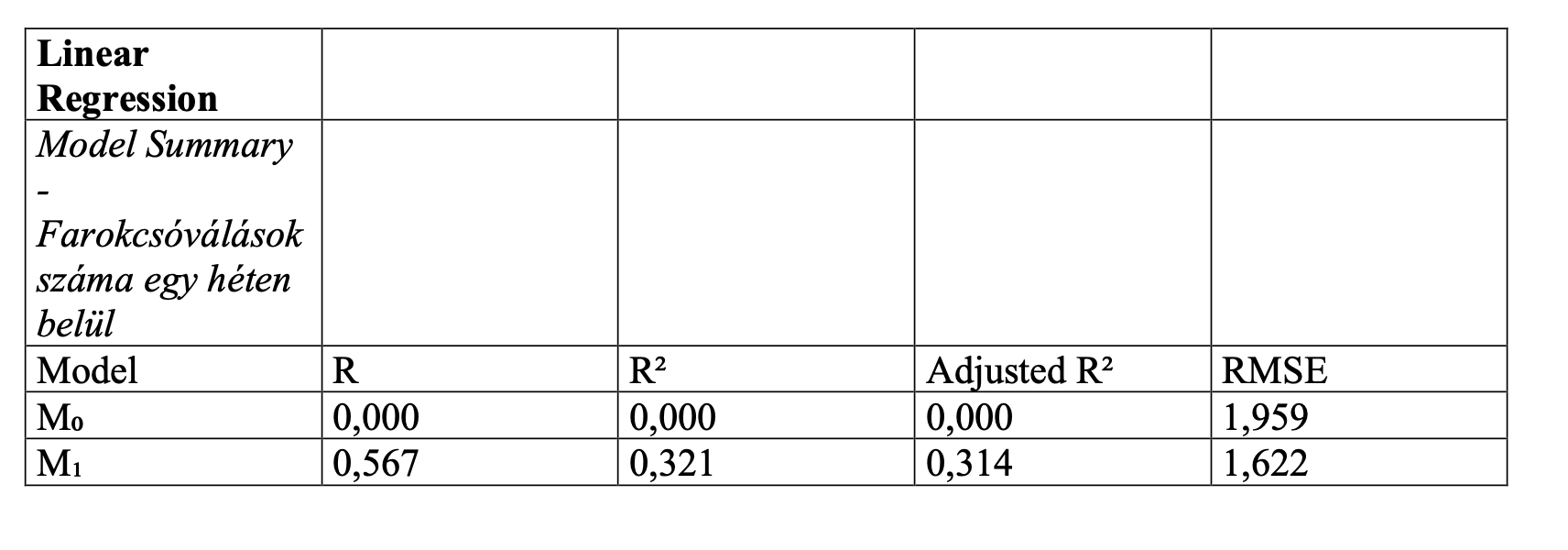
Ugye az elején mondtam, hogy a lineáris regresszió nem csak azt mutatja meg, hogy van-e összefüggés, hanem azt is, hogy mekkora.
A modell summary táblázatban látható az R2 és az adjusted (korrigált) R2 érték. Az R2 érték azt mutatja meg, hogy a független változó (vagy más néven prediktor változó) hány százalékát magyarázza a függő változónak. Pl. ha az R2 érték 0,9 (ami extrémen magas, akkor már gyanús), akkor 90%-át. Az adjusted R2 pedig a populációra korrigált R2 érték, általában minimális eltérés van. (Ha túl magas, akkor az vagy ilyen nagyon hard science esetekben van, pl. orvostudomány, de ilyen pszichológia, közgazdaságtan etc. esetében ha ilyen magas lenne, fennállna az ún. multikollinearitás veszélye. Ez a szempontunkból irreleváns, csak elmondom, fun fact :D)
Ha az R2 érték gagyi, pl. 10 százalék alatti, akkor a harmadik táblázatra, azaz a koefficiens táblázatra felesleges tovább menni. Tehát elmondjuk, hogy nagyon gyenge kapcsolat van, a hipotézist nem sikerült igazolni, és kész. De ha ez az érték meghaladja a 0,1-et, azaz a 10%-ot, akkor folytathatjuk az elemzést, és megnézzük a 3. táblázatot is!
Koefficiens táblázat
3) Ha egy, az ANOVA F-teszt p-értéke is szignifikáns volt; és kettő, ezt követően az R2 érték sem volt full gagyi (tehát minimum 0,1), akkor jön a koefficiensek, vizsgálhatjuk azokat is.
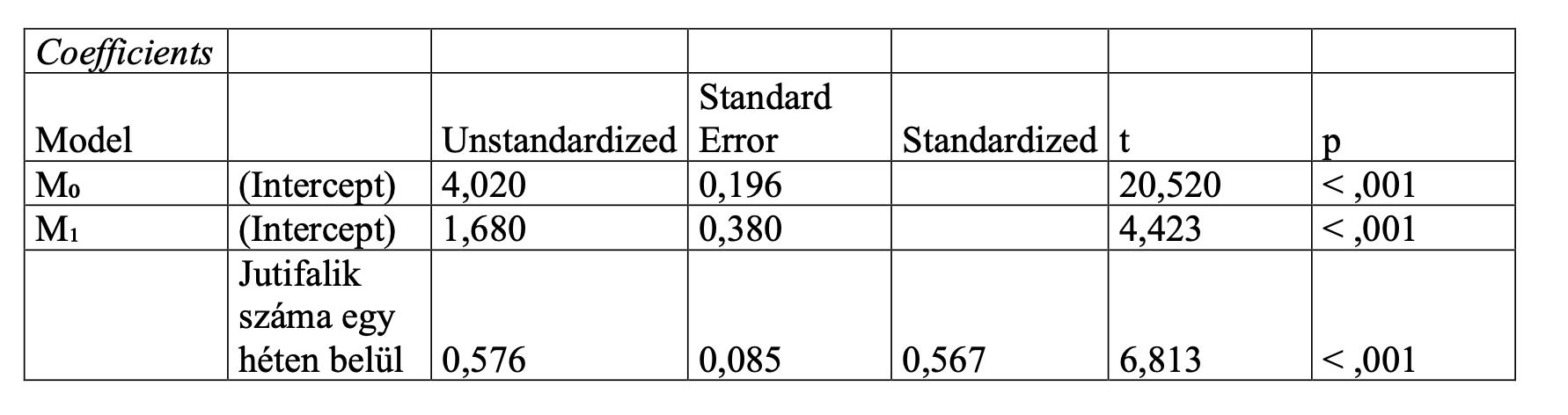
Az eredeti nevén standardized oszlop, vagyis a béta, azt mutatja meg, hogy a prediktor milyen irányba befolyásolja a függő változót. Ha negaív, akkor éppen ellentétes irányba mozognak, ha pozitív, akkor egy irányba. Mit jelent ez a példánkban? Tehát, valaki minél több jutifalit ad (magas értékeket adott meg) annál többet csóválja a házi kedvence a farkát egy héten. (hiszen azokra az állításokra nagyobb értékeket válaszolt). Tehát az egyik esetben magasabb, és a másikban is magasabb értékeket adott.
Gyakorlatilag ennyi, itt elég ennyit tudni, negatív, vagy nem. Ez persze csak akkor ér valamit, ha a mellette található p-érték szignfikáns. Ez a példánkban, mint látható, szignifikáns a p-érték (kisebb, mint 0,05), tehát sikerült igazolni az eredményeket. A p-érték jelentéséről itt írtunk.
A többi lineáris regresszió elemzésekor ugyanígy kell eljárni. Tehát:
ANOVA-táblázat (főként p-érték)
R2 érték
béta (vagy ahogy az output eredetileg elnevezi, "standardized") érték.
Ez persze egy leegyszerűsített leírás, tehát ha őszintén érdekel a statisztika, ennél többre van szükség. De ahhoz, hogy a dolgozatban összefoglald egy lineáris regressziós számítás eredményeit, bőven elegendő.
